Intel launched the Pentium processor in 1993. Unfortunately, dividing sometimes gave a slightly wrong answer, the famous FDIV bug. Replacing the faulty chips cost Intel $475 million. I reverse-engineered the circuitry and can explain the bug. 1/9
|
54 comments
The table is stored in a circuit called a PLA (Programmable Logic Array). A PLA stores logic equations in two grids of transistors: the "AND plane" and the "OR plane". Logic equations are defined by putting a transistor (or not) at each grid point. This is much more compact than a ROM: 112 rows instead of 2048. 3/9 @kenshirriff I kinda want to see if you can patch the fdiv bug with a FIB edit now... @azonenberg @kenshirriff The question I had was, if those 16 entries had been specified correctly in the input to the code that derived the PLA equations ... would that still have fit in the same size (112 rows) of PLA? If not, you'd need more than a FIB to fix this. @acsawdey @kenshirriff Yep, that's exactly the question. How extensive the edits are. @azonenberg @kenshirriff hadn't considered that, yeah maybe it fits but you have to change some large percentage of the logic terms. @acsawdey @kenshirriff The other thing is, you can't FIB a transistor into being. It's easy (ish) to FIB a metal rom in either direction, and to delete a transistor in an active-programmed ROM. But you can't make new ones. @azonenberg I'd have to study the PLA equations carefully to see if zapping a few transistors would expand the "2" region enough to cover the missing cells. Without looking, I'd give it 50-50 odds of working since it depends on the exact bit patterns. @azonenberg I did some analysis and yes, you could patch the fdiv bug with about 6 FIB edits. By removing transistors, you can expand existing PLA terms to cover the missing table entries. What makes it work is that the unused table entries don't need to be 0, so you have a lot of flexibility. If you needed to change just the bad entries, you'd be stuck. I studied the transistor grids under a microscope and extracted the pattern. From this, I reverse-engineered the lookup table for division. The photos show a small part of the grids. A transistor is formed by a polysilicon line crossing doped silicon. No crossing, no transistor. 4/9 Smart mathematicians figured out Pentium's division algorithm and the missing entries in 1995 by examining the pattern of errors. But I can confirm it in silicon. Moreover, I see 16 missing entries in the table, not just 5, but 11 of them don't cause errors due to luck. 5/9 Intel claimed the bug was due to an error in a script to download the entries into the PLA. But due to the 16 missing entries, I think they made a mathematical error in constructing the table, misjudging the effect of a 7-bit adder. Here's the adder, just above the PLA. 6/9 You'd expect that Intel fixed the problem by adding the 5 missing entries. Instead, they filled *all* the unused entries with 2's. This made the table easier to store in a PLA, shrinking it by 1/3. The fixed PLA has lots of unused rows at the bottom. 7/9 Intel said the FDIV bug was unimportant, but the public disagreed. Newspapers and TV discussed the bug. Intel claimed the bug would happen every 27,000 years; IBM said every 24 days and stopped selling Pentiums. Intel gave in and replaced Pentiums at a cost of $475 million. 8/9 I hope to have a blog post with more details on the Pentium FDIV bug soon. Until then, you can read about the Pentium Navajo rug: https://oldbytes.space/@kenshirriff/113063183366751314 But I made that bug happen a bunch of times in Lotus 123 (I don't think I had Excel at the time) when I was a kid. So pretty often if you tried! And I remember getting a clockspeed upgrade (60 -> 90 MHz iirc) when Intel sent us a new CPU. @ElsaPreme The Pentium division bug is deterministic, so you can make it happen all day long if you do a particular division. The lesser-known 386 multiplication bug, on the other hand, was a circuitry issue that depended on the voltage, frequency, and temperature, so it was unpredictable. @johnlogic @kenshirriff that was surprisingly just for a big corporation, if true! Yes; I was impressed with this interviewee's story alleging that Intel had had an internal lightning strike. @johnlogic I've talked with a few people who worked on the Pentium and I don't think anyone got fired over it. In "The Pentium Chronicles", the error is blamed on a flawed formal proof that misled the testers into thinking a change was safe. @kenshirriff I can imagine they didn't want to move any other block, given that may have meant relaying stuff out and having to do some timing checking etc, so expanding the PLA might have been hard @kenshirriff Fascinating details, thanks! Is there any chance there could have been an intentional reason to create this bug? For example, would it weaken any encryption algorithms at the time, make the chips cheaper to produce, make money on stock shorts for the uncovered failure or any other scenario that was on purpose? @kenshirriff oooooo that's a neat bit of trivia Cool work, thanks for sharing :D @kenshirriff I went to a talk c. 2003 from a sr. Intel person who gave a description I have not heard anywhere else: There was a die size push and somebody said "I can make the divider smaller and here is a mathematical proof that it's correct." People were so impressed by the proof they didn't notice that it was wrong and didn't care that the space savings were inconsequential (he described it as "taking out Missouri doesn't make the US smaller" 😂). This meshes nicely with you missing entries. @kenshirriff this reminds me of some old HP PCBs I once bought at a surplus shop. They had rows and columns of traces on top and bottom, and diodes placed to form a ROM pattern. On the semiconductor, I would expect that these would be MOS transistors each with one side connected to its base, making each effectively a diode. @cr1901 @kenshirriff @fatlimey @kenshirriff That will have to wait until I re-derive how to do square roots by hand again. For the 4th time. Would be nice to commit it to memory and my ego refuses to look it up :D. @cr1901 @kenshirriff The way to think about it is the quotient is trying to be the square of your current output, and the difference between that and your input guides selection of your next digit. @kenshirriff@oldbytes.space huh, neat! i note that this looks similar to (but not quite the same as) the balanced base representation which is found sometimes in algorithms used in prime number hunting to perform arithmetic on large numbers @kenshirriff - How does one acquire the skills to even start doing this? How does one then use those skills to be able to afford to do this :)? @clark Learning to do this is mostly a matter of patience and reading old VLSI books. Also, you need a metallurgical microscope, which shines light down through the lens. A regular biological microscope won't work since the light comes from below. @kenshirriff An Intel and a Motorola chip talks to each other @curved_ruler @kenshirriff at university I had an account on one of the first dual-processor Linux boxes. Of its CPUs, one had that FDIV bug, and one didn't. That meant a userland process could detect when it was migrated between CPUs, by doing a hardware division operation that the two CPUs would answer differently. The admin of the machine spent a lot of time in ytalks with Linus Torvalds, because Linux was just starting to develop its SMP support at the time, and he could provide useful statistical data! @simontatham @kenshirriff this whole thread was fascinating but this tidbit is the icing on the cake. @stylus It's kind of complicated and depends on a very unlikely sequence of carries. The bad cells are almost but not quite impossible to reach. The divider uses a carry save adder, which holds the carry bits instead of propagating them . If these bits are just right, you hit the bug. @kenshirriff I received a nice 486Dx2 at the start of uni, and had the luck of being a poor student during the Pentium's prime years. By the time I was working and had money for a new computer, the Pentium II was out, and I was happily edge-slotting it into a new system. @kenshirriff At a textiles exhibit at the National Gallery of Canada in Ottawa last weekend, I saw this piece by Navajo/Dine artist Marilou Schultz, who was contracted by Intel to weave a replica of the Pentium CPU in 1994. Full transcript of the info card is in the Alt text.
@kenshirriff I think I wrote an ML program com file using debug to test for that in less than 10 bytes. The windows patch couldn't stop it. |

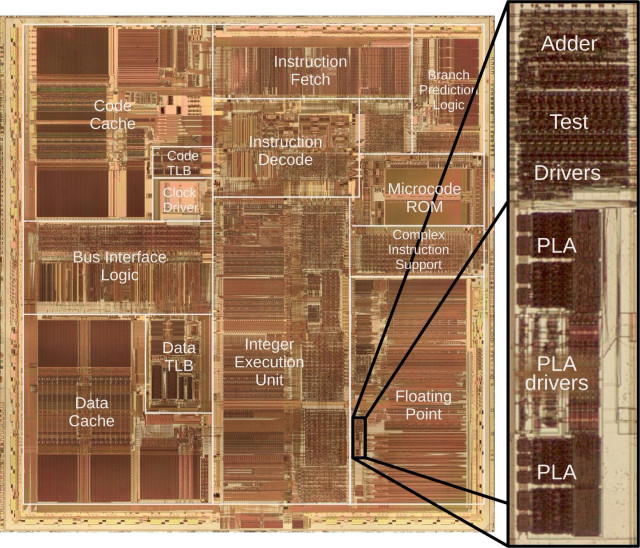



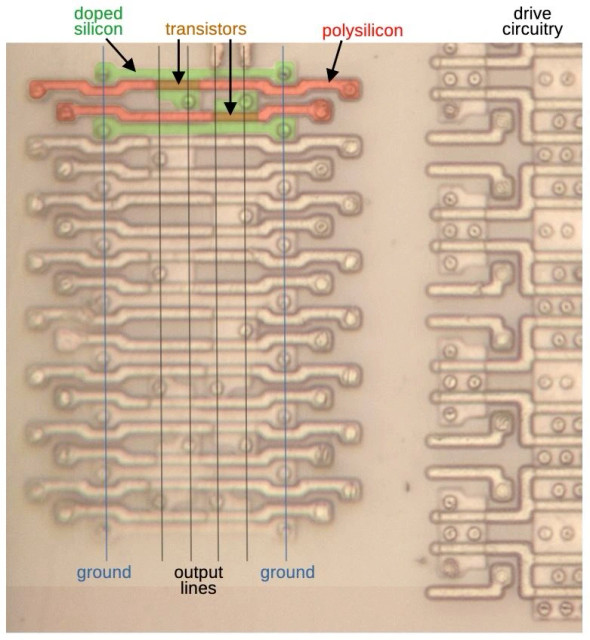
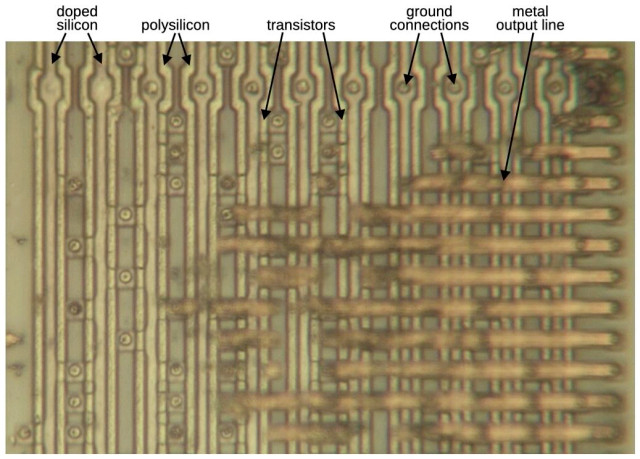


























The Pentium uses a division algorithm called SRT. It generates two bits at a time, making division twice as fast. SRT's secret is quotient digits can be negative: -2, -1, 0, 1, 2. A 2048-entry table gives the digit for a particular divisor and remainder. Unfortunately, 5 entries (red) were wrong. 2/9